moving coil step-up transformers explained

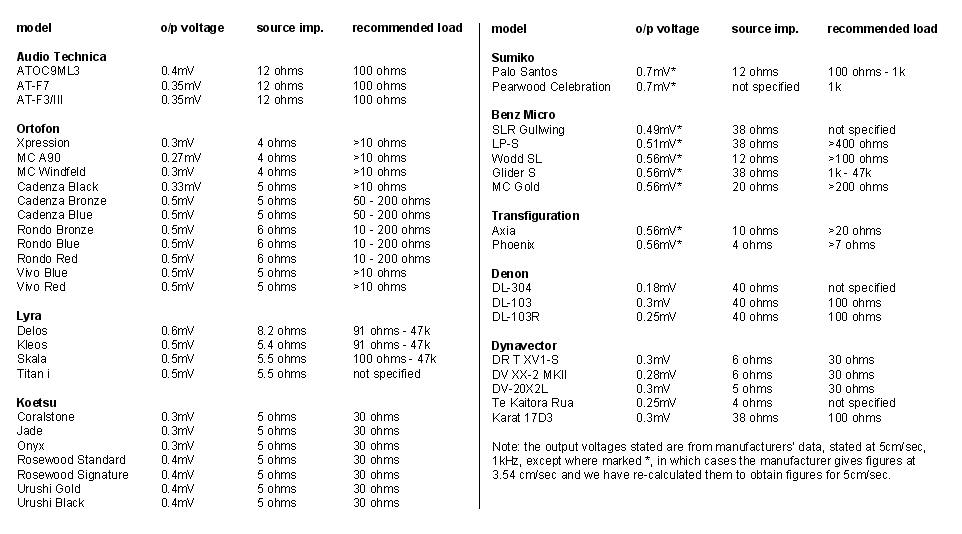
Step-up transformers for moving coil cartridges are the most esoteric and misunderstood items in the world of hi-fi, and this partly explains why they are so seldom used. This is a great shame because the use of a good transformer gives the best possible performance from a moving coil cartridge. This article is intended to demystify the subject and allow the reader to select a suitable transformer with confidence. Apologies in advance if some of the maths becomes a bit baffling and causes more confusion rather than less. Despite the apparent complexity, the conclusions are quite simple and you could just skip to the bottom of the page for the recommendations.
For information about transformers specifically for Denon cartridges, click here.

the cartridge operating principle
Moving magnet cartridges, as their name implies, contain magnets which are moved by the stylus’ cantilever, and the movement induces the signal voltage in fixed coils in close proximity to the magnets. In moving coil cartridges the roles are reversed, so now the magnets are fixed and the coils move. The big advantage of moving coils is that the coils are much lighter than the magnets, so they are much more responsive to the motion of the stylus.
The big disadvantage is that the output voltage of moving coil cartridges is about 20dB lower than that of moving magnets, so an extra 20dB of gain is required. The extra gain can be provided by the phonostage amplifier, by an external device called a headamp, or by a transformer. The most commonly found solution is to increase the gain in the phonostage, but step-up transformers are still the best solution where cost is no object.

why use a transformer at all?
It used to be the case that a good signal-to-noise ratio was impossible to achieve from a moving coil cartridge without a step-up transformer. An extra 20 or 30 decibels of gain wasn’t a problem, but doing so with low noise using valves, transistors or op-amps was a problem. Modern transistors and op-amps can now offer much better signal-to-noise ratios but valves still usually need transformers to work successfully with low output moving coil cartridges. An alternative to the step-up transformer is the headamp (or pre-preamp). This is a transistor or op-amp amplifier which raises the output of moving coil cartridges up to moving magnet level. Rothwell offer the Headspace as a high quality, low noise headamp.
Apart from the issue of noise, the sound quality of transformers is something their advocates swear by. The distortion produced by audio transformers is of a completely different nature to that produced by a transistor amplifier. The harmonic distortion in transformers is greatest at the lowest frequencies and falls rapidly as the frequency rises, whereas in transistor amplifiers distortion more usually rises as the frequency rises. More importantly, intermodulation distortion tends to be lower in transformers than it is transistor amplifiers. The outcome is that although transformers aren't absolutely free of distortion (nothing is), the distortion is very benign compared to the distortion produced by many transistor amplifiers. This explains why the sound produced when a moving coil cartridge is used with a good transformer is so sublime and can create an open and spacious soundstage with amazing separation between instruments.
The case against transformers is simply one of cost. Transistors can be as cheap as a few pennies (or less when bought in sufficient quantities) whereas transformers always cost a lot more, by as much as a factor of several thousand, due to the expensive materials used in the core and the cost of the copper windings in terms of both material and labour.

cartridge loading
Before considering how to match a moving coil cartridge with a transformer, it is worthwhile considering the effects of different loads on moving coil cartridges.
When any signal source is connected to any load impedance a potential divider is formed by the source's output impedance and the load impedance. (The output impedance is also know as the source impedance or internal impedance. The load impedance is also known as the input impedance.) The signal source could be a phono cartridge, microphone, CD player, mixer etc., it doesn't matter. The load could be a phonostage, mixer, transformer, or simply a resistor – again, it doesn't matter. The potential divider formed by the source and load impedances acts as an attenuator or a pre-set volume control. If the load impedance is very much bigger than the source impedance the attenuation is low and the effective pre-set volume control is near maximum. The usual rule for audio equipment in general is to feed the signal into a load at least ten times greater than the source impedance to avoid any significant signal loss, and this is applies to moving coil cartridges as much as to anything else. If the load impedance is 10 times greater than the source impedance the signal lost by the “pre-set volume control” is less than 1dB, ie nearly all the signal generated by the source is available to the following amplifier. Any loss of signal at the source/load interface is usually considered a bad thing as it compromises the signal-to-noise ratio. More signal is lost, ie the pre-set volume control is turned down more, if the load impedance isn't significantly higher than the source impedance. When the source and load impedances are equal the signal loss is 6dB. When the source impedance is 9 times greater than the load impedance the signal loss is 20dB. Most modern moving coil cartridges have a source impedance of about 10 ohms and the “load impedance ten times the source impedance” rule suggests 100 ohms is a good choice for load impedance and causes less than 1dB of signal loss. This is well in line with the recommendations from many cartridge manufacturers (see the table of data below). Anything above 100 ohms should be equally suitable.
Does the cartridge's tonal balance change with load impedance? It certainly does if the cartridge is a moving magnet type, but low output moving coil cartridges are much less sensitive to changes in the load impedance. Users sometimes claim that higher load impedances produce a brighter sound than lower ones, but cartridge manufacturers tend be non-specific about recommended load impedances, often recommending a wide range or simply anything above a minimum impedance.
The recommendation of Rothwell Audio Products is in line with Ortofon, Audio Technica and most other cartridge manufacturers - that 100 ohms is a good value for most cartridges, and that the exact value is not critical as long as it is well above the cartridge's source impedance.
One thing is certain, and that is that the load impedance should not be equal to the cartridge's source impedance. That would produce a 6dB loss of signal (when there's often only a few hundred microvolts to start with) and seriously compromise the signal-to-noise ratio. The idea that having the load impedance equal to the source impedance achieves perfect "matching" is wrong and is the most commonly held myth about moving coil cartridges. It also gives rise to most of the confusion surrounding step-up transformers and how to select the correct one for any given cartridge. The reasons for the “matched impedance” myth are examined below.

the transformer turns ratio and impedance ratio
The turns ratio of a transformer is the ratio of the number of turns of wire on the primary winding to the number of turns of wire on the secondary winding, and the voltage on the primary is stepped up (or down) by the same ratio as the turns ratio and appears on the secondary. A transformer with a 1:10 turns ratio for example will step up a voltage at its primary by a factor of ten. However, since transformers are totally passive devices with no power supply to draw energy from, no extra power can be produced by a transformer and an increase in voltage will be accompanied by a corresponding decrease in current. This is what gives rise to the concept of the impedance ratio. The impedance ratio is the square of the turns ratio and makes an impedance on the secondary winding of a transformer appear to a source feeding the primary as that impedance transformed by the square of the turns ratio. The transformer itself doesn't have an impedance, rather an impedance on one side of it will look like a different impedance from the other side (it works in both directions). In the case of, for example, a 1:10 step-up transformer, a 20k impedance on the secondary winding will appear to be a 200 ohm impedance on the primary winding (20,000 divided by 10 squared equals 200). A 1:2 step-up transformer with a 100k load on the secondary would appear to have an input impedance to a source driving the primary as 25k (100k divided by 2 squared equals 25k).

So, it would seem logical that a cartridge with an output voltage of, for example, 0.5mV, when used with a step-up transformer with a 1:10 turns ratio, would produce 5mV at the transformer's output. Yes, it would if the cartridge's source impedance (also known as its internal impedance or its coil impedance) was zero. In practice, with low impedance cartridges of about 10 ohms or less and low ratio transformers (less than about 1:20), the transformer's output voltage is very close to the cartridge's output voltage multiplied by the turns ratio and can be safely used as a good first order approximation for guidance. However, the cartridge's source impedance may be low but it is never zero, and the transformed secondary load needs to be considered for a more accurate analysis. Consider as an example a transformer with a 1:10 ratio and a cartridge with a 10 ohm coil. If the load on the transformer secondary is an MM phonostage with a 47k impedance, that load appears to the cartridge as 470 ohms (47,000 divided by 10 squared) and must be driven by the 10 ohm coil. The 470 ohm load and the 10 ohm source form a potential divider (the “pre-set volume control” described in the previous section) with some of the cartridge's voltage dropped across its own internal 10 ohm impedance. The proportion dropped internally is 10/(470+10) = 0.0208, which is not very much at all – just 0.2dB. The deviation from the first order approximation is small and probably not worth worrying about, but it is there. It's when higher turns ratios are used with higher source impedances that the potential divider effect becomes significant. Consider a cartridge with a 40 ohm coil and a transformer with a 1:30 ratio. The 47k load on the secondary now appears as 52 ohms from the primary side. When driven by a 40 ohm source the voltage divider is formed by 52 ohms and 40 ohms. Therefore the proportion of signal dropped across the cartridge's coil is 40/(40+52) = 0.43, which is very significant – nearly half the voltage produced by the cartridge is lost internally. Whereas only 0.2dB was lost in the previous example, here the signal loss is 5dB, and instead of achieving a signal voltage at the output of the transformer of 30 times the cartridge's output, the output is only 0.43x30 times the cartridge's output, ie a voltage step-up of effectively just 13 times, not 30 times. Clearly, increasing the transformer turns ratio by a factor of X doesn't increase the output voltage by the same factor. As the turns ratio increases, the increase in the output voltage gets less and less as the load on the cartridge becomes more and more significant until a point is reached where increasing the turns ratio further actually causes the output voltage to drop.
The point at which the maximum possible voltage at the transformer's output is achieved occurs when the transformed load is equal to the source impedance. In the case of a 47k secondary load (the usual load impedance of an MM phonostage) and a 40 ohm MC cartridge, the turns ratio would have to be 1:34.28 to get the absolute maximum output voltage. This is because 40x34.28x34.28 = 47000
It’s this that gives rise to the misguided notion that the transformer must “match” the cartridge impedance. Yes, it may be true that matching the impedances gives the maximum possible voltage at the transformer's output, but in a hi-fi system we're not looking for the absolute maximum voltage from the transformer, we're looking for a voltage suitable to be fed into the following MM phonostage and we're looking for maximum fidelity. This rarely (if ever) achieved by matching the impedances. The signal voltage suitable for an mm phonostage to handle is about 5mV. A higher voltage into the phonostage will reduce headroom and increase distortion. A lower voltage will compromise the signal-to-noise ratio. Trying to achieve 5mV into the phonostage (with maximum fidelity) should be the aim of a step-up transformer.
The big mistake most often made when selecting a transformer for a moving coil cartridge is to overlook the voltage required at the phonostage's input and instead try to make the impedances match so that, for example, a cartridge with a 5 ohm source impedance sees a 5 ohm load at the transformer's input. This approach takes the cartridge's impedance as the most important factor when in reality it should be the cartridge's output voltage.

To demonstrate how far wrong the “matched impedance” approach can be, take as an example an Ortofon Vivo Red cartridge with a 5 ohm source impedance. In order to "match the impedance”, the 47,000 ohms on the secondary side of the transformer would have to appear as 5 ohms on the primary side. That means that the impedance ratio must be 9400 (because 47,000 divided by 5 equals 9400) and therefore the turns ratio must be the square root of 9400, which is 97. So we must find a step-up transformer with a turns ratio of 1:97. However, the Vivo Red's output voltage is 0.5mV and the voltage fed to the phonostage by a 1:97 transformer would 24mV. That would be enough to overload most phonostages and would be a long way from optimal. A much better approach to finding a suitable transformer ratio would be to work with the cartridge's output voltage. The Vivo Red has an output of 0.5mV and the phonostage requires about 5mV for the best performance, therefore a ratio of 1:10 would appear to be much better. The first order approximation suggests a 1:10 ratio would give us 5mV. Does that still hold true if we also consider the cartridge's 5 ohm source impedance and the load impedance presented by the transformer? Yes. A 1:10 transformer with a 47k load on its secondary winding presents a load of 470 ohms to the cartridge. The voltage divider formed by the 5 ohm source impedance and the 470 ohm reflected load means that only 5/(470+5) is dropped across the cartridge's internal impedance and the actual voltage at the transformer's output is 4.95mV, ie extremely close to the estimate using the approximate method. The 470 ohm load seen by the cartridge is perfectly compatible with Ortofon's recommended load of >10 ohms. The “impedance matching” method of using a 1:97 ratio transformer would give the cartridge a 5 ohm load impedance, which is outside the manufacturer's recommendation. Also, for the reasons explained below, a 1:97 transformer would have a seriously compromised performance compared to a 1:10 transformer.

Now consider a different cartridge, the Dynavector Karat17D3 with a 38 ohm coil. Using the impedance matching approach to find the best transformer ratio we end up with a ratio of 1:35 and the cartridge's 0.3mV output becomes 5.25mV at the the transformer's output. This time, the “impedance matching” approach appears to have worked out well, but is is really the best turns ratio? Maybe not, because Dynavector's recommended load is 100 ohms and a 1:35 transformer would give the cartridge a 38 ohm load. In this instance a lower turns ratio would be better. For example, a 1:20 transformer would give the cartridge a load of 117.5 ohms and have an output of 4.5mV. Also, a 1:20 transformer is likely to have better performance than a 1:35 transformer, as explained below.

real world transformers
The calculations above assume perfect transformers. That means transformers wound with wire of zero resistance, with zero capacitance between windings, with zero leakage inductance, with infinite primary inductance etc, etc., resulting in a wide bandwidth covering at least 20Hz - 20kHz. However, in the real world, we have to live within the constraints nature places upon us and work with materials that do have resistance, capacitance, etc. All transformers have limitations, and those with higher step-up ratios tend to have more limitations than those with lower step-up ratios. This is because a higher ratio requires more turns of wire on the secondary winding, and more turns means more resistance and more capacitance between windings. These factors combine with any leakage inductance and cause the transformer's high frequency response to be compromised. This usually takes the form of ringing on the waveform (see below) and an earlier roll-off of high frequencies.
Alternatively, to preserve the high frequency response, a higher turns ratio could be achieved by having fewer turns of wire on the primary, but that reduces the primary inductance and compromises the transformer's low frequency response. As a general rule, when all other factors are equal, a lower step-up ratio gives better performance than a higher step-up ratio. Quite often a lower step-up ratio giving only 1dB or 2dB less output can yield a much wider bandwidth. For the best possible performance, choose a lower turns ratio if possible.

transformer loading
The idea that optimum performance comes from matching the impedance of the load to the cartridge's impedance (shown above to be somewhat hit-and-miss) also gives rise to another fallacy – that of transformer loading. The misguided theory, sometimes advocated on websites and forums, says that a loading resistor on the transformer's secondary winding can be used to “correctly load the cartridge” or to “match the transformer to the cartridge”. This is a very dubious theory indeed, so lets analyse what is really happening. Take as an example the Ortofon Vivo Red cartridge examined above (5 ohm source impedance, 0.5mV output voltage). As has already been determined, a 1:10 transformer will give us the voltage we require for an MM phonostage, but the advocates of “correct loading” may be convinced that the cartridge performs best with a particular load, despite the manufacturer's recommended load being anything over 10 ohms. So what is “the correct load”? Often, it is claimed to be the same as the cartridge's source impedance, hence “matching” is achieved. As shown above, a turns ratio of 1:97 will present a 5 ohm load to the cartridge, but what if such a transformer cannot be found? What if the nearest transformer available is 1:36? Can that be made to “match the cartridge correctly”? The transformer with a normal 47k load would give the cartridge a load of 36 ohms (and produce an output voltage of 15.8mV). In order to make this transformer match the cartridge with a load impedance at the primary of 5 ohms, a load on the secondary of 6480 ohms could be employed instead of the 47k normally found on an MM phonostage. This would not only produce a load impedance for the cartridge of 5 ohms, it would also reduce the output voltage to 9mV. Has the additional loading resistor now made the system optimal? No, it hasn't. The cartridge is now seeing half the minimum impedance which the manufacturer recommends and the signal voltage into the MM phonostage is still enough to reduce its headroom significantly. Clearly, this isn't optimal, but it is a lot better than it was with a 1:36 transformer and no additional loading resistor. Anyone who is taking an empirical approach to optimising their system and experimenting with loading resistors based on the idea of “impedance matching” as advocated on some websites would conclude (understandably) that their system now sounds better because “the cartridge is loaded correctly”. In fact it sounds better because the phonostage is being overdriven less than it was before. It would be better still if a 1:10 transformer was used instead of trying to make a transformer with far too high a turns ratio “match” anything by fudging it with resistors.
The “correct loading” or “load matching” myths are fuelled further by a fortuitous by-product of loading the transformer with an additional resistor – damped ringing, analysed in more detail below..

Transformer ringing
All transformers have limitations due to the inevitable capacitance between windings, leakage inductance etc. and these determine the transformer’s bandwidth and can produce “ringing”. Ringing can be seen as overshoot at the corners of a squarewave, as illustrated in the figures above. A lower load impedance on the transformer's secondary winding has two effects: reduced output and damped ringing. This perhaps explains why people attempting to tune their system by ear have reported that loading resistors (intended to load the cartridge correctly) have a beneficial effect. However, in reality the improvement in sound quality isn't due to the cartridge being loaded correctly, it's due to the phonostage being overdriven less, and due to transformer ringing being damped.
A much better approach to optimising sound quality would be to separate the two issues and deal with them individually. Overloading the phonostage would be addressed by using a transformer with a lower turns ratio, and that alone would have the added benefit of better performance. Ringing can be dealt with by employing a suitably chosen resistor-capacitor network without the penalty of excessive signal loss. In the case of the Ortofon Vivo Red in the example above, a reduction in output voltage is a benefit, but more often than not it isn't a benefit. With cartridge's such as the Denon DL-304 with its feeble 0.18mV output, any loss of signal voltage caused by attempting to damp ringing with a resistor is unwelcome. Achieving the correct signal level is one issue and damping transformer ringing is another. Trying to treat both issues with one cure isn’t advised. Fortunately, ringing can be damped by a suitably chosen resistor-capacitor network without the penalty of a reduction in output.

The oscilloscope screen shots in figure 1 above illustrate ringing and the effects of different loads on the transformer's secondary winding.
Figure 1a shows the output with a 47k ohm load on the secondary of a fairly modest transformer. The slope on the top and bottom of the waveform is caused by the low frequency limit of the transformer due to inadequate primary inductance. The peaks at the corners of the waveform are due to transformer ringing, also known as overshoot. Figures 1b, 1c and 1d show what happens to the waveform when the secondary load is reduced to 22k, 10k and 5k1 respectively. The slope of the waveform straightens out as the impedance is reduced and the corners lose the unwanted peaks, but the overall signal level also drops significantly. The level with the 5k1 load is about 10dB less than the level with the 47k load. This shows that although the performance of the transformer can be improved by reducing the load impedance, the benefit comes at the expense of a serious loss of signal level. Since the point of using a step-up transformer with a moving coil cartridge is to gain an extra 20dB or so of signal level, any loss due to incorrectly loading the transformer is unacceptable.

The transformer ringing which can be seen as peaks at the corners of the waveform in figure 1 is a common problem and arises from inductive and capacitive elements (leakage inductance and inter-winding capacitance) combining to produce resonance. The capacitance of the cable connecting an mc step-up transformer to the following phonostage also plays a part, which is why the interconnecting cable should be a low capacitance design and kept as short as is practical. Ringing can be found in many commercial moving coil step-up transformers, regardless of price. Sometimes the ringing occurs at very high frequencies and is reasonably well damped and therefore quite benign, but often it occurs at a much lower frequency or rings for such a long period that it can cause quite audible effects. Even expensive transformers from well-known audiophile brands often exhibit poor performance as regards ringing.

Figure 2 below shows oscilloscope screen shots of a step-up transformer from a manufacturer of expensive valve amplifiers. The input signal is again a 1kHz square wave from a 10 ohm source. Figure 2a shows the transformer's output when there is no load and the overshoot is quite clear to see. Figures 2b to 2e show the 1kHz waveform with different loads on the transformer's secondary. A 47k load has barely any effect on ringing, but as the load is reduced through 22k, 10k and 5k1, the ringing is progressively damped. At 5k1, the ringing is gone but the signal level is reduced. With this particular transformer, the signal loss with the 5k1 load is not as bad as the signal loss suffered by the first transformer, but any loss of signal should be avoided. Note however that the top and bottom of the waveform are very flat, indicating that this transformer has very good low frequency performance. Figure 3 is a closer look at the corner of the waveform and shows clear ringing which lasts for several cycles before subsiding. The frequency of the ringing is about 100kHz - well above audibility - so there's no chance of actually hearing a ringing sound, but it is clear that the signal produced by the signal generator is being severely deformed. Figure 4 shows the output from a 10kHz square wave input. The waveform is hardly recognisable as a square wave at all and it is not difficult to imagine what effect such deformation could have on a music signal. The leading edges of crash cymbals, ride cymbals and snare drums or the attack of plucked strings could easily lose integrity and become a confused jumble of sound. When several percussive instruments are playing together, as is very common, separation between the instruments will not be helped by the severe ringing shown in figure 4.

Fortunately, ringing can be totally eliminated without sacrificing signal level by loading the secondary winding correctly with a resistor-capacitor network, not a simple resistor (though far too many commercial step-up transformers totally neglect this). Although lower values of resistive load on the secondary do tend to reduce ringing, as illustrated above, loading with a correctly optimised resistor/capacitor network will produce far superior results. Since different transformers are constructed with different core materials, wire thickness, number of turns and winding techniques, the optimum load network will be different for each, and the only way to determine the correct network is through measurement.
Figure 5 below shows the transformer of figures 2 and 3 after an optimised load network has been applied, again with a 1kHz square wave input. The ringing has been eliminated and the signal level available into a 47k load has been maintained.
Figure 6 shows the effect of applying a non-optimum loading network. In this case the incorrect component values (out by only a few nanofarads and a few kilohms) have resulted in quite a peculiar deformation of the waveform. This illustrates the need to get the loading network right rather than copying a network which is optimised for a different transformer.
As an aside, the use of silver wire for the windings might appear impressive but does little or nothing for performance due to the fact that silver has only marginally less resistance than copper and the limiting factors in transformer performance are due to the finite size and permeability of the core, leakage inductance and inter-winding capacitance, none of which are improved by the use of silver wire. However, it does have a significant impact on cost. It should go without saying that elaborate cases with 3D milled aluminum front panels or gold plated turrets, while very nice to look at, also have no benefit for audio performance but, again, do have an impact on cost.

listening tests and empirical results
You will find much ill-informed advice on the internet (on any subject). Often incorrect conclusions have been drawn from empirical trials and misleading advice formulated, such as when loading resistors have been added to the secondaries of step-up transformers. Yes, performance improved. No, it wasn't because the cartridge impedance was matched to anything. Sometimes laws of physics have been misinterpreted. Yes, the transformer ratio that makes the load impedance equal to the source impedance gives the maximum voltage. No, that doesn't give you the highest fidelity performance.
There are various articles on websites which state or imply that the audible effects of altering the load on a transformer's secondary winding are due to the different transformed loads seen by the moving coil cartridge. In an article about step-up transformers on the 6moons website (http://www.6moons.com/audioreviews/stepup/primer.html) Tom Miccolis states "...you may wish to experiment with lowering the primary impedance value in order to witness what affect it has on the resultant sound from your system. This can be accomplished by using resistors in parallel across the secondary side of the transformer."
Quite true, but resistors in parallel across the primary side of the transformer would also load the cartridge. Why not do that instead? No explanation is given. The most likely explanation is that any audible differences produced by the loading resistors are due to reduced output and reduced ringing, ie changes to the transformer's performance, not changes to the cartridge's performance. The same article contains other errors and misleading information, such as stating step-up ratios as 20:1 instead of 1:20, and much worse, stating that "resistor loading can cause ringing on the signal". On the contrary, resistor loading damps ringing, not causes it, as is clearly illustrated in the screen shots above.
In truth, a step-up transformer can only be fully optimised with a very specific load on its secondary. If it works open circuit or into too high a load impedance, it will almost certainly display ringing on its output. If it works into too low an impedance, it will not suffer from ringing on its output but will possibly have a reduced high frequency response and the signal voltage will not be stepped up as much as it would be otherwise.
This is borne out by experiments and listening tests, even by people who do not fully understand the technicalities of transformer loading. In another article about step-up transformers on the internet (http://www.high-endaudio.com/RC-Step-ups.html), Arthur Salvatore concludes that transformer loading is crucial to optimising performance (quite true) and after describing the results of his empirical experiments with resistor loading the Bent Silver transformer he states that "when the resistor value is too high, the sound will normally be bright, forward, light and lean" and goes on to say that "when the resistor value is too low, the sound will normally be dark, recessed and compressed". He also says that with a slightly reduced load impedance the sound had "greater separation", but reducing the resistor value too far caused the volume to drop too much.
All of Mr Salvatore's results were predictable and all concur with results of the transformer loading experiments described above. At first the reduced load impedance is damping out the ringing in the transformer and causing the sound to become clearer and less bright sounding. Further reductions in the load cause the high frequencies to balance better with the low frequencies (as predicted by the square wave flattening out in figure 1 above) and reducing the load impedance even further causes the signal level to drop to such an extent that the transformer is no longer stepping up sufficiently to be any use. The correct way to load the transformer would have been with a resistor/capacitor network, which, in fairness, the author does allude to, and which could have eliminated ringing and maintained the step-up ratio. Nevertheless, his empirical results concur very well with both theory and measurement.

the transformer/cartridge selection method recommended by Rothwell
Bearing in mind that the MM phonostage amplifies voltage, not impedance, it's the cartridge's output voltage which is important, not the impedance. A cartridge with a source impedance of 3 ohms does not require a turns ratio significantly different from a cartridge with a source impedance of 20 ohms if their output voltages are the same. Take as examples the Ortofon Vivo Red and the Audio Technica ATOC9ML3. The Ortofon has a source impedance of 5 ohms and the Audio Technica has a source impedance of 12 ohms. The impedances differ by a factor of 2.4. Does that mean the turns ratios for the two cartridges should differ by 2.4? Or 2.4 squared? No, their output voltages are almost the same at 0.5mV and 0.4mV and in both cases a 1:10 transformer will give an output voltage suitable for an MM phonostage to handle. A quick “times ten” calculation gives output voltages of 5mV and 4mV. A more precise analysis (taking into account the different source impedances) shows the precise output voltages will be 4.95mV and 3.9mV, ie almost the same as the quick calculation. In fact, all the calculations above are probably unnecessary in practice. The majority of modern low output moving coil cartridges can be used successfully with transformers in the range 1:10 to 1:20. It really is as simple as that. Higher turns ratios than 1:20 are not recommended because output voltages start to get too high, load impedances start to get too low, bandwidth starts to shrink, or some combination of the three starts to limit performance. Lower turns ratios than 1:10 are not recommended because the voltage step-up would be too low to be beneficial. (However, some of the cartridges labelled as “high output moving coils” can benefit from low ratio transformers of about 1:3.)

Aim for about 5mV into the phonostage and look for the turns ratio which will produce that with the cartridge in question. Too high a voltage will compromise headroom (though bear in mind that valve designs have huge headroom), and too low an output will result in a compromised signal/noise ratio. 5mV is a good target figure to aim for. The range from 4mV to 6mV covers a +/- 3dB spread either side of 5mV. The range from 3mV to 8mV covers a +/- 4.5dB spread around the 5mV target. Don't worry about trying to get exactly 5mV, and adjust your calculations accordingly if your phonostage is more sensitive than usual. If your phonostage states its sensitivity as 3.5mV for example, use that as your target figure instead of 5mV. Having found a likely match using just the cartridge output voltage and transformer turns ratio, you can check that the transformed impedance is acceptable, though it almost certainly will be. Assuming a standard MM phonostage load of 47k, a turns ratio of 1:10 will give the cartridge a load impedance of 470 ohms and a turns ratio of 1:20 will give the cartridge a load impedance of 117.5 ohms (in the absence of any load modifying components).

further examples
The table below shows the specifications for a range of modern low output moving coil cartridges. The use of modern rare earth magnets has resulted in most moving coil cartridges having a reasonably healthy output of around 0.4mV or 0.5mV whilst maintaining a low source impedance. This makes the signals they produce much easier to handle than the cartridges from 40 years ago (neodymium magnets weren't invented until 1983) so the problems of yesteryear are thankfully not such a problem now.

All the Audio Technicas will work well with 1:10 transformers and produce enough voltage for a typical MM phonostage. They will also work well with 1:20 transformers, producing voltages of 7.3mV, 6.4mV and 6.4mV respectively.
The first four Ortofons on the list with output voltages below 0.4mV will work well with 1:10 transformers and 1:20 transformers. The ones with outputs of 0.5mV will work well with 1:10 transformers. 1:20 transformers could be used where the phonostage can accommodate an input voltage of 9.6mV. 9.6mV is 5.7dB higher than 5mV, but MM phonostages should have 20dB headroom or more.
The Dynavectors would also work well with 1:10 transformers or 1:20 transformers.

The Denons are unusual in having high source impedances but quite low output voltages. A more detailed analysis of Denon cartridges can be found here, but the summary is that 1:20 is a good ratio for them.

Lyra make excellent cartridges but their recommended loadings appear confusing. On their website they say that the recommended load "directly into MC phono input : 91ohms - 47kohm", but then go on to say "recommended load via step-up transformer : 5 - 15 ohm". Taken literally, this makes no sense, but probably means the transformer should be designed for a source impedance of 5 - 15 ohms rather than presenting a load of 5-15 ohms to the cartridge. Whatever they mean, their cartridges work well with 1:10 transformers.

Finally, there are many cartridges made before about 1990 which have much lower outputs than the modern cartridges in table 1 above (below 0.2mV). In theory they should be used with higher step-up ratios than 1:20, but experience has shown that 1:20 is still sufficient in many cases. The superior performance of lower turns ratios remains attractive and transformers with significantly higher ratios should be approached with caution. The author has encountered one mc step-up transformer with a turns ratio of 1:100. Its bandwidth with a 10 ohm source was well below 20kHz.

Rothwell Transformers
The MC1 has a step-up ratio of 1:12.9, the MCX has a step-up ratio of 1:10 and the MCL has a step-up ratio of 1:20. In all cases the input impedance is 100 ohms. This is because loading is used on the primary side of the transformer as well as the secondary side to maintain a 100 ohm load. The extra load makes the input impedance compatible with a very wide range of cartridges and has the added benefit of smoothing out any non-linearities in the input impedance caused by the real-world practicalities of transformer design such as non-zero leakage inductance and interwinding capacitance.
The secondary windings of both the MC1 and MCL have optimised loading networks so that when fed into a 47k moving magnet phonostage the bandwidth and voltage gain are maximised and ringing eliminated. Do not use any additional loading on the secondary of the MC1, MCX or MCL in order to try to improve cartridge loading or cartridge matching as prescribed by dubious advice found on the internet.
The MCX and MCL are both premium quality devices with very quality core materials and sophisticated winding techniques giving there transformers a wide bandwidth and good hum rejection.
The MC1 is an entry level transformer, but still capable of very good performance.

Headamps
An alternative way to raise the output of moving coil cartridges to the same level as moving magnet cartridges is to use a headamp. These are active amplifiers, not transformers, and first became popular in the late 1970s/early 1980s. The advantage of a headamp over a transformer is that the gain and load impedance can be set independently of each other and a very wide bandwidth is possible. The disadvantage of headamps is that their noise performance is inferior to step-up transformers. Though good ones can come close, poor ones fall a long way short.
Since MC compatible solid-state phonostages became commonplace, standalone headamps have almost completely disappeared, but Rothwell do offer high quality, low noise headamp called the Headspace as an alternative to using a step-up transformer..

summary
1) Output voltage and source impedance are clearly defined parameters of a cartridge, but the recommended load impedance is not. A load impedance which is equal to the cartridge’s source impedance does not mean that the cartridge is perfectly matched to the load to optimum performance.
2) Phonostages amplify voltage, not impedance. The signal voltage at the phonostage’s input is more important than the load impedance seen by the cartridge.
2) Turns ratios of less than 1:10 are usually too low to step up the cartridge’s output sufficiently.
3) Turns ratios of more than 1:20 are usually too high to be compatible with most modern cartridges and should be used only with certain cartridges of very low output.
4) Loading the transformer does have an effect on the load seen by the cartridge, but any change in sound quality is more likely to be due to altering the performance of the transformer, not the cartridge.
5) Complicated calculations involving impedance transformations and specific recommended loads are usually unnecessary.

further reading
an excellent article is available from the website of Jensen transformers. 
http://www.jensen-transformers.com/application-notes/
Look for “Audio Transformers - Bill Whitlock chapter 11” You now have to register on the Jensen’s website before downloading anything, however this article is excellent and can be taken as gospel. It is quite technical.

FAQs about magnetic sheilding
http://www.magnetic-shield.com/faq/interference.html

A detailed paper about core materials
www.sowter.co.uk/pdf/GAVS.pdf
This is probably way more information and detail than you need, but you may find it interesting

Lundahl’s Transformer Design Philosophies
http://www.lundahl.se/pdfs/papers/design_philosophies.pdf
Lundahl supply the transformers used in the MCL